적분공부해야할수도.
'공부'에 해당되는 글 48건
- 2017.12.01 적분 공부
- 2017.11.14 전기화학 공부
- 2017.11.02 와트 Watt (W) 일
- 2017.11.02 용어 공부
- 2017.11.02 양자화
- 2017.10.29 페르미입자
- 2017.10.29 한국진공학회 진공이야기
- 2017.10.29 광자, 포톤(photon)
- 2017.10.29 일함수
- 2017.10.29 화학용어집
http://www.wizmac.com/2015/lecture/board01_view.htm?No=172&Sub_No=8
'공부' 카테고리의 다른 글
| 광전 효과 ,일함수 (0) | 2017.12.01 |
|---|---|
| 적분 공부 (0) | 2017.12.01 |
| 용어 공부 (0) | 2017.11.02 |
| 페르미입자 (0) | 2017.10.29 |
| 한국진공학회 진공이야기 (0) | 2017.10.29 |
이온화에너지
원소의 이온화 에너지란 어떤 화학 원소의 기체상태의 원자1mol에서 전자 1mol을 떼어 내는 데 필요한 에너지를 뜻한다.
전자친화도
전자 친화도(電子親和度, electron affinity)는 원자나 분자가 전자 하나를 얻어 에너지준위가 낮아지면서 방출하는 에너지를 말한다. [1] 전자 친화도가 클수록 그 입자는 전자를 얻기가 더 쉬운 것으로 해석된다.
'공부' 카테고리의 다른 글
| 적분 공부 (0) | 2017.12.01 |
|---|---|
| 전기화학 공부 (0) | 2017.11.14 |
| 페르미입자 (0) | 2017.10.29 |
| 한국진공학회 진공이야기 (0) | 2017.10.29 |
| 광자, 포톤(photon) (0) | 2017.10.29 |
quantization 양자화 되어있다.
연속적이지않고 어느 임의의 한 값을 가지고 있다.
이런 뜻인거 같다.
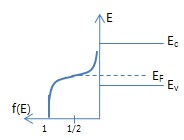
1. 페르미 입자, 페르미 통계 이란? ㅇ 페르미 입자 (Fermion) 또는 페르미 기체(Fermi gas) - 페르미 통계를 따르는 입자 (전자,양성자,중성자 등) . 파울리의 배타원리를 따르고, 구별불가능한 입자들 ㅇ 페르미 통계 (Fermi statistics) - 페르미 입자 계가 따르는 통계적 성질 (☞ 통계역학 참조) ※ 페르미(Enrico Fermi,1901~1954) : 이탈리아 물리학자 - 반도체 등 고체에서 전하입자(전자,홀)의 존재를 에너지에 대한 점유 분포 확률로써 통계역학적 방법으로 제시함 (1926) 2. 페르미 함수 또는 페르미-디락 함수 (Fermi-Dirac function) ㅇ 특정 양자 상태를 전자가 채울 확률을 에너지의 함수 f(E)로 표현한 것 - 열평형상태에서 허용된 에너지 준위를 차지할 전자들의 분포 함수 - 에너지 E 상태가 전자에 의해 점유될 확률 함수 (점유확률). EF : 페르미 에너지 (Fermi Energy) 또는 페르미 준위 (Fermi Level) .. 열평형상태 하에 페르미함수 f(E)가 1/2이 되는 에너지준위 . k : 볼츠만 상수 . T : 절대온도 ㅇ 근사 - 큰 값의 E (E-EF≫kT) => 볼츠만 근사(Boltzmann approximation) . f(E) ≒ e-(E-EF)/kT - 낮은 값의 E (E-EF≪kT) . f(E) ≒ 1 .. 낮은 에너지 상태들은 전자들에 의해 완전히 점유되어짐 3. 맥스웰 볼츠만 근사 (Maxwell Boltzmann Approximation) ㅇ E-EF ≫ kT - f(E) ≒ e-(E-EF)/kT
4. 점유확률 f(E)와 반도체 에너지밴드 구조 사이의 관계 ㅇ 진성 반도체
ㅇ n-type 반도체
ㅇ p-type 반도체
4. 입자 계의 성질에 따른 통계적 확률분포 구분 ㅇ 맥스웰-볼츠만 통계 (Maxwell–Boltzmann Statistics) ☞ 맥스웰볼츠만분포 - 고전적 통계 - 구별성 : 구별 가능한 동일 입자 (입자 간에 충분히 떨어져 있으므로 서로 구별 가능함) - 제한성 : 각 에너지 상태에 들어가도록 허용되는 입자의 수에 제한이 없음 - 대상 : 이상 기체 분자 등 ㅇ 보즈-아인슈타인 통계 (Bose–Einstein Statistics) - 양자역학적 통계 - 구별성 : 구별 불가능한 입자 - 제한성 : 각 에너지 상태에 들어가도록 허용되는 입자의 수에 제한이 없음 - 대상 : 파울리 배타 원리에 지배되지 않는 입자 (영이나 정수 스핀 값을 갖는 입자) * 例) 광자의 행동, 흑체복사 등 . 보손(Boson), 스핀 1의 입자, 이들 집단은 Bose–Einstein statistics을 따름 ㅇ 페르미-디락 통계 (Fermi–Dirac Statistics) ☞ 페르미 분포함수 - 양자역학적 통계 - 구별성 : 구별 불가능한 입자 - 제한성 : 하나의 에너지 상태에 오직 하나의 입자 만 들어가도록 허용됨 - 대상 : 파울리 배타 원리를 따르는 입자 (½에 홀수 정수 배가 곱해진 스핀 값을 갖음) * 例) 전자,양성자,중성자 등 . 페르미온(Fermion), 스핀 ½ 입자, 이들 집단은 Fermi–Dirac statistics을 따름
출처
http://www.ktword.co.kr/abbr_view.php?nav=&m_temp1=4617&id=612
http://www.ktword.co.kr/abbr_view.php?nav=&m_temp1=4463&id=732
'공부' 카테고리의 다른 글
| 전기화학 공부 (0) | 2017.11.14 |
|---|---|
| 용어 공부 (0) | 2017.11.02 |
| 한국진공학회 진공이야기 (0) | 2017.10.29 |
| 광자, 포톤(photon) (0) | 2017.10.29 |
| 비문학 지문읽기!!! (0) | 2017.09.13 |
 한국진공학회 2016_12_03 광전자 분광현미경학.pdf
한국진공학회 2016_12_03 광전자 분광현미경학.pdf
 한국진공학회 2017_03_01_색즉시공 공즉시색.pdf
한국진공학회 2017_03_01_색즉시공 공즉시색.pdf
 한국진공학회 2017_03_08 강력한 흡입력을 갖는 진공청소기.pdf
한국진공학회 2017_03_08 강력한 흡입력을 갖는 진공청소기.pdf
공부한거...
출처 http://www.kvs.or.kr/
'공부' 카테고리의 다른 글
| 용어 공부 (0) | 2017.11.02 |
|---|---|
| 페르미입자 (0) | 2017.10.29 |
| 광자, 포톤(photon) (0) | 2017.10.29 |
| 비문학 지문읽기!!! (0) | 2017.09.13 |
| 반도체 관련 (0) | 2017.09.07 |
2.1. 광자[편집]
光子, photon
빛(전자기)은 입자성과 파동성을 가진다. 이 중 빛의 입자성을 가리키는 빛의 또 다른 이름이 바로 광자다. 빛의 파동성을 가리키는 이름은 전자기파다.
쉽게 설명하자면, 빛이란 건 전자기력이 작용하는 역장(=전자기장)을 쉽게 부르는 이름이다. 근데 이 전자기장은 과학자들이 관측하기에 따라 입자처럼 보일 때도 있고 파동처럼 보일 때도 있다. 광자란 이 빛의 입자스러움을 가리키는 명칭.
2.1.1. 설명[편집]
일단 빛이기 때문에 당연히 광속으로 운동한다. 광자의 에너지는 [1]이다. 또한, 광자는 운동량 를 갖는다.
전자기 상호작용을 매개하는 게이지 보손. 질량과 전하가 없고, 스핀이 1이다. 광자에 질량이 없다는 말에 "에너지는 곧 질량이므로 에너지를 가진 광자도 질량을 갖게 된다."고 답하는 경우가 많은데, 광자에 질량이 없다고 말할 때의 질량은 정지 질량이므로, 보통 상황에서는 굳이 그렇게 세세하게 따질 필요가 없다.
광자와 같이 질량이 없는 입자를 룩손이라고 하며, 룩손은 무조건 광속으로 움직인다. 룩손 이외의 입자는 광속보다 느리거나 한없이 가까워질 수는 있을지언정, 결코 광속으로 움직이지는 못한다. 질량이 없으므로 중력의 직접적인 영향을 받지 않기에, 광자의 이동방향의 휘어짐, 즉 빛의 휘어짐은 중력에 의한 시공간 왜곡의 강력한 증거가 된다.
아이작 뉴턴은 빛이 입자로 이루어져있다고 주장하였으나, 그러한 설명으로는 빛의 파동적인 성질(대표적으로 간섭현상)을 설명하지 못하므로, 초기에는 뉴턴의 권위에 의해 빛의 입자설과 파동설이 대립하다가 19세기 초 토마스 영의 이중슬릿실험에 의해 빛이 파동임을 보여 주고, 제임스 맥스웰이 빛이 전자기파임을 밝혀내고 전자기파의 속도가 빛의 속도와 근사함을 증명하여 파동설이 정설로 인정되기까지 했다.
그 후 1859년 말에서 1860년초 키르히호프(G. Kirchhoff, 1824-1887)에 의해 '흑체복사'에 대한 이론이 등장하였다. 한 물체가 뜨거워지면 열을 내게 되는데, 이를 복사(radiation)라고 부르며, 키르히호프는 '복사는 물질이나 빈구멍(Cavity)의 모양, 크기와는 상관이 없고 오직 온도와 빛의 파장에만 관계된다는 것이다'는 것을 밝혀냈다. 즉, 같은 온도로 달구어진 물체는 어떤 물질이든 방출하는 빛의 분포가 똑같다는 것이다. 특히 표면에 부딪히는 모든 복사를 흡수하는 경우 이런 물체를 흑체(black body)라고 부르는데, 이런 특징은 파동성과 아울러 입자성을 지니고 있을 가능성을 보여준다. 19세기말 물리학자들은 고체에서 방출되는 복사를 조사하여 여러 가지 파장 또는 진동수를 가진 빛으로 구성되어 있음을 알게 되었고, 표면의 온도와 빛의 파장이 어떠한 관계에 있는가를 연구하면서 아인슈타인에 의해 양자화에 대한 논의가 시작되었다.
20세기 초에 고전적인 흑체는 무한히 빛을 방출해야 한다는 문제가 발견되었고, 이를 해결하기 위해 막스 플랑크는 파동의 에너지가 양자(量子)화된 것이 빛이라는 가설을 도입하였다.[2]
알베르트 아인슈타인은 1905년에 빛이 입자로 구성되었을 경우 광전효과를 설명할 수 있다는 사실을 보였고, 이후 양자역학의 발전과 양자전기역학의 도입으로 빛의 양자화를 이론적으로 설명할 수 있게 되었다.
출처
https://namu.wiki/w/%EA%B2%8C%EC%9D%B4%EC%A7%80%20%EB%B3%B4%EC%86%90?from=%EA%B4%91%EC%9E%90#s-2.1
'공부' 카테고리의 다른 글
| 용어 공부 (0) | 2017.11.02 |
|---|---|
| 페르미입자 (0) | 2017.10.29 |
| 한국진공학회 진공이야기 (0) | 2017.10.29 |
| 비문학 지문읽기!!! (0) | 2017.09.13 |
| 반도체 관련 (0) | 2017.09.07 |
Work Function 일 함수 | (2017-03-21) |
1. 일함수 (Work Function) ㅇ 금속 표면으로부터 전자 1개를 떼어내는데 필요한 에너지 - 페르미 준위와 진공 준위와의 에너지 차이 . 페르미 준위에서 진공 준위까지 전자를 떼어내는데(여기하는데) 필요한 에너지 ※ 물질에서 전자방출과 빛의 상호작용 ☞ 광전효과 참조 2. 금속 및 반도체 일함수 ㅇ 금속 - 각각의 금속 종류에 따라 그 값이 정해짐 . 금속 일함수 값 例) Ag : 4.26, Al : 4.28, Au : 5.1, K : 2.30, Na : 2.75, Hg : 4.49, Ni : 5.15, W : 4.55 [eV] ㅇ 도핑된 반도체 - 도핑 농도에 따라 페르미준위가 변하므로 일률적으로 정해지지 않음※ 금속과 달리 반도체 페르미 준위는 전자가 없는 금지대역 내에 있으므로, - 금속 일함수와 직접 비교하기에는 어려움 ☞ 플랫밴드 참조 ※ ☞ 금속 반도체 접합 참조 3. 전자친화도,이온화에너지,일함수,전기음성도 비교 ※ 원자 간 고립,결합 상태 성질에 따른 구분 ㅇ 고립 상태인 원자의 성질 - 이온화 에너지 : 개별 중성원자로부터 전자 하나를 떼내는데 필요한 최소 에너지 - 전자친화도 : 중성원자에 전자 하나를 더해서 음이온을 만들기위한 에너지 ㅇ 결합 상태인 원자의 성질 - 일함수 : 금속 표면으로부터 전자 1개를 떼어내는데 필요한 에너지 . 금속 내 전자들이 전자 바다를 형성하며 결합하고 있는 인력의 척도 - 전기음성도 : 결합된 원자(분자)가 공유 전자쌍을 끌어당기는 능력 수치 . 例) HF(불화수소) 분자는 극성 공유결합을 함 .. 전기음성도가 더 큰 F 원자로 음 전하가 집중되고, .. 전기음성도가 작은 H 원자쪽은 양 전하를 띄게 됨
출처 http://www.ktword.co.kr/abbr_view.php?m_temp1=4457