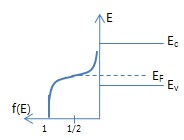
1. 페르미 입자, 페르미 통계 이란? ㅇ 페르미 입자 (Fermion) 또는 페르미 기체(Fermi gas) - 페르미 통계를 따르는 입자 (전자,양성자,중성자 등) . 파울리의 배타원리를 따르고, 구별불가능한 입자들 ㅇ 페르미 통계 (Fermi statistics) - 페르미 입자 계가 따르는 통계적 성질 (☞ 통계역학 참조) ※ 페르미(Enrico Fermi,1901~1954) : 이탈리아 물리학자 - 반도체 등 고체에서 전하입자(전자,홀)의 존재를 에너지에 대한 점유 분포 확률로써 통계역학적 방법으로 제시함 (1926) 2. 페르미 함수 또는 페르미-디락 함수 (Fermi-Dirac function) ㅇ 특정 양자 상태를 전자가 채울 확률을 에너지의 함수 f(E)로 표현한 것 - 열평형상태에서 허용된 에너지 준위를 차지할 전자들의 분포 함수 - 에너지 E 상태가 전자에 의해 점유될 확률 함수 (점유확률). EF : 페르미 에너지 (Fermi Energy) 또는 페르미 준위 (Fermi Level) .. 열평형상태 하에 페르미함수 f(E)가 1/2이 되는 에너지준위 . k : 볼츠만 상수 . T : 절대온도 ㅇ 근사 - 큰 값의 E (E-EF≫kT) => 볼츠만 근사(Boltzmann approximation) . f(E) ≒ e-(E-EF)/kT - 낮은 값의 E (E-EF≪kT) . f(E) ≒ 1 .. 낮은 에너지 상태들은 전자들에 의해 완전히 점유되어짐 3. 맥스웰 볼츠만 근사 (Maxwell Boltzmann Approximation) ㅇ E-EF ≫ kT - f(E) ≒ e-(E-EF)/kT
4. 점유확률 f(E)와 반도체 에너지밴드 구조 사이의 관계 ㅇ 진성 반도체
ㅇ n-type 반도체
ㅇ p-type 반도체
4. 입자 계의 성질에 따른 통계적 확률분포 구분 ㅇ 맥스웰-볼츠만 통계 (Maxwell–Boltzmann Statistics) ☞ 맥스웰볼츠만분포 - 고전적 통계 - 구별성 : 구별 가능한 동일 입자 (입자 간에 충분히 떨어져 있으므로 서로 구별 가능함) - 제한성 : 각 에너지 상태에 들어가도록 허용되는 입자의 수에 제한이 없음 - 대상 : 이상 기체 분자 등 ㅇ 보즈-아인슈타인 통계 (Bose–Einstein Statistics) - 양자역학적 통계 - 구별성 : 구별 불가능한 입자 - 제한성 : 각 에너지 상태에 들어가도록 허용되는 입자의 수에 제한이 없음 - 대상 : 파울리 배타 원리에 지배되지 않는 입자 (영이나 정수 스핀 값을 갖는 입자) * 例) 광자의 행동, 흑체복사 등 . 보손(Boson), 스핀 1의 입자, 이들 집단은 Bose–Einstein statistics을 따름 ㅇ 페르미-디락 통계 (Fermi–Dirac Statistics) ☞ 페르미 분포함수 - 양자역학적 통계 - 구별성 : 구별 불가능한 입자 - 제한성 : 하나의 에너지 상태에 오직 하나의 입자 만 들어가도록 허용됨 - 대상 : 파울리 배타 원리를 따르는 입자 (½에 홀수 정수 배가 곱해진 스핀 값을 갖음) * 例) 전자,양성자,중성자 등 . 페르미온(Fermion), 스핀 ½ 입자, 이들 집단은 Fermi–Dirac statistics을 따름
출처
http://www.ktword.co.kr/abbr_view.php?nav=&m_temp1=4617&id=612
http://www.ktword.co.kr/abbr_view.php?nav=&m_temp1=4463&id=732
'공부' 카테고리의 다른 글
| 전기화학 공부 (0) | 2017.11.14 |
|---|---|
| 용어 공부 (0) | 2017.11.02 |
| 한국진공학회 진공이야기 (0) | 2017.10.29 |
| 광자, 포톤(photon) (0) | 2017.10.29 |
| 비문학 지문읽기!!! (0) | 2017.09.13 |